Insight learning is a type of learning that happens suddenly, in the flash of a moment. It’s those “a-ha” moments, the light bulbs that people typically get long after they’ve abandoned a problem.
It’s believed that insight learning has been behind many creative inventions, discoveries, and solutions throughout history.

In this article, we’ll explore what’s behind those “a-ha” moments. We’ll look at how we learn, how we solve problems, and how insight fits into the picture of problem-solving.
Associative learning vs Insight learning
Behavioural psychologists in the mid-twentieth century had come up with good theories of how we learn by association. Their work was largely based on Thorndike’s experiments, where he put animals in a puzzle box with many levers on the inside.
To get out of the box, the animals had to hit the right lever. The animals randomly moved levers before they figured out which one opened the door. This is associative learning. The animal associated the movement of the right lever with the opening of the door.
As Thorndike repeated the experiments, the animals got better and better at figuring out the right lever. In other words, the number of trials required by the animals to solve the problem decreased over time.
Behavioral psychologists are infamous for not paying any attention to cognitive processes. In Thorndike’s, Pavlov’s, Watson’s, and Skinner’s experiments, the subjects learn things purely from their environments. There’s no mental work involved except association.
Gestalt psychologists, on the other hand, were fascinated by how the brain could perceive the same thing in different ways. They were inspired by optical illusions such as the reversible cube shown below, which can be perceived in two ways.
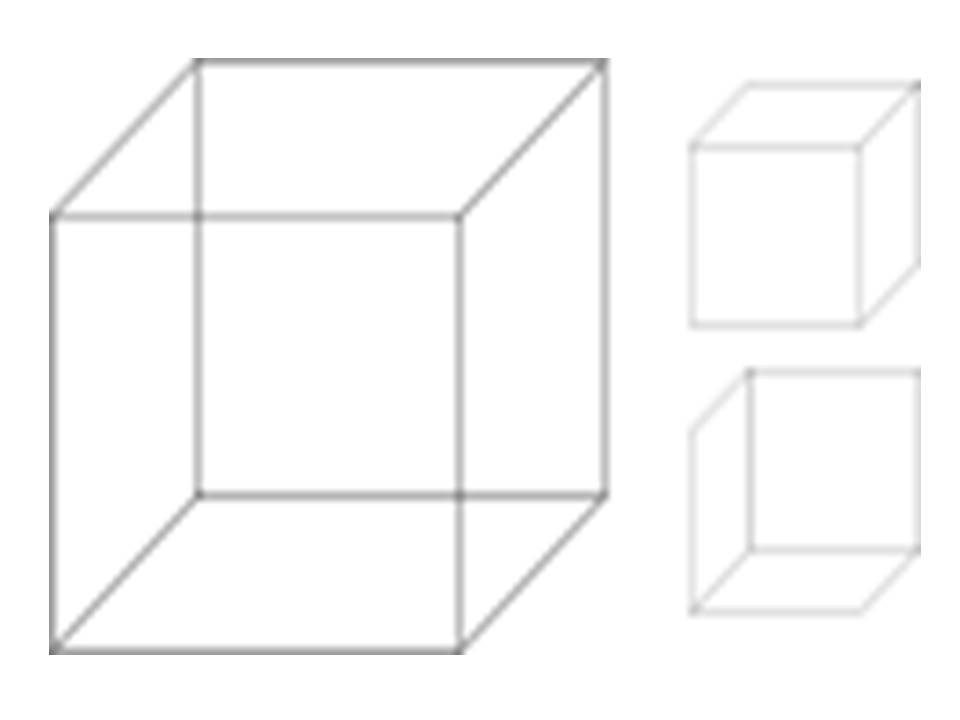
Instead of focusing on the parts, they were interested in the sum of the parts, the whole. Given their interest in perception (a cognitive process), Gestalt psychologists were interested in the role cognition could play in learning.
Along came Kohler, who observed that apes, after they couldn’t solve a problem for a while, had sudden insights and seemed to figure out the solution.
For example, to reach bananas that were out of their reach, the apes joined two sticks together in a moment of insight. To reach a bunch of bananas hanging high from the ceiling, they placed crates that were lying around on top of each other.
Clearly, in these experiments, the animals didn’t solve their problems with associative learning. Some other cognitive process was going on. Gestalt psychologists called it insight learning.
The apes didn’t learn to solve the problems purely by association or feedback from the environment. They used reasoning or cognitive trial-and-error (as opposed to behaviorism’s behavioral trial-and-error) to arrive at the solution.1
How does insight learning occur?
To understand how we experience insight, it’s helpful to look at how we solve problems. When we encounter a problem, one of the following situations may arise:
1. The problem is easy
When we encounter a problem, our mind searches our memory for similar problems we’ve faced in the past. Then it applies solutions that have worked in our past to the current problem.
The easiest problem to solve is the one you’ve encountered before. It might take you only a few trials or just one trial to solve it. You don’t experience any insight. You solve the problem by reasoning or analytic thinking.
2. The problem is harder
The second possibility is that the problem is a bit harder. You probably have faced similar, but not too similar, problems in the past. So you apply solutions that have worked for you in the past to the current problem.
However, in this case, you need to think harder. You need to re-arrange elements of the problem or restructure the problem or your approach to solving it.
Eventually, you solve it, but in more trials than were required in the previous case. You’re more likely to experience insight in this case than in the previous one.
3. The problem is complex
This is where people mostly experience insight. When you encounter an ill-defined or a complex problem, you exhaust all the solutions you can derive from memory. You hit a wall and you don’t know what to do.
You abandon the problem. Later, when you’re doing something unrelated to the problem, a flash of insight appears in your mind that helps you solve the problem.
We usually solve such problems after a maximum number of trials. The more trials a problem takes to solve, the more you have to re-arrange the elements of a problem or restructure it.
Now that we have contextualized the insight experience, let’s look at the stages involved in insight learning.
Stages of insight learning
The stage decomposition theory of Wallas2 states that the insight experience involves the following stages:
1. Preparation
This is the analytic thinking stage in which the problem-solver tries all kinds of approaches to solving a problem using logic and reasoning. If the solution is found, the next stages don’t occur.
If the problem is complex, the problem-solver exhausts their options and cannot find a solution. They feel frustrated and abandon the problem.
2. Incubation
If you’ve ever abandoned a difficult problem, you must have noticed that it lingers in the back of your mind. So does some frustration and a slight bad mood. During the incubation period, you don’t pay much attention to your problem and engage in other routine activities.
This period can last from a few minutes to many years. Studies have shown that this period increases the probability of finding the solution.3
3. Insight (Illumination)
Insight occurs when the solution manifests spontaneously in conscious thought. This suddenness is important. It seems like a leap to the solution, not a slow, step-wise arrival to it as in analytic thinking.
4. Verification
The solution reached via insight may or may not be correct and so needs to be tested. Verifying the solution, again, is a deliberative process like analytic thinking. If the solution found via insight turns out to be false, then the Preparation stage is repeated.
I know what you’re thinking:
“It’s all fine and dandy- the stages and everything. But how exactly do we get insights?”
Let’s talk about that for a moment.
The Explicit-Implicit Interaction (EII) theory
An interesting theory put forward to explain how we get insights is the Explicit-Implicit Interaction (EII) theory.4
The theory states that there’s a constant interaction that happens between our conscious and unconscious processes. We’re rarely fully conscious or unconscious when interacting with the world.
Conscious (or explicit) processing largely involves rule-based processing that activates a specific set of concepts during problem-solving.
When you’re solving a problem analytically, you do it with a limited approach based on your experience. The brain’s left hemisphere handles this type of processing.
Unconscious (or implicit) processing or intuition involves the right hemisphere. It activates a broad range of concepts when you’re trying to solve a problem. It helps you look at the big picture.
When you learn to ride a bicycle for the first time, for example, you’re given a set of rules to follow. Do this and don’t do that. Your conscious mind is active. After you’ve learned the skill, it becomes part of your unconscious or implicit memory. This is called implicitation.
When the same thing happens in reverse, we have explicitation or insight. That is, we get insight when unconscious processing transfers information to the conscious mind.
In support of this theory, studies have shown that just before having an insight, the right hemisphere sends a signal to the left hemisphere.5
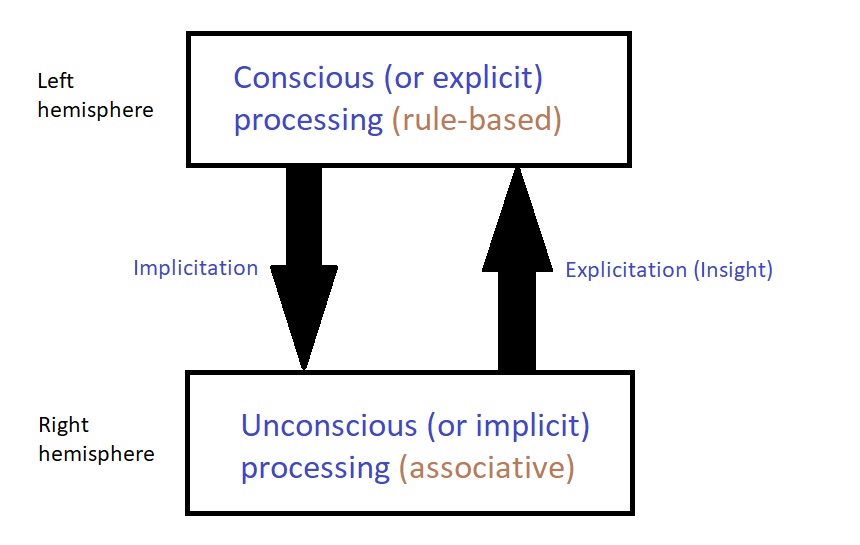
The above figure tells us that when a person abandons a problem (i.e. inhibits conscious processing), their unconscious still tries to make associative connections to reach the solution.
When it finds the right connection- voila! The insight appears in the conscious mind.
Note that this connection may arise spontaneously in the mind or some external stimulus (an image, sound or a word) might trigger it.
I’m sure you’ve experienced or observed one of those moments where you’re talking to a problem-solver and something you said triggered their insight. They look pleasantly surprised, ditch the conversation, and rush to solve their problem.
Further insights into the nature of insight
There’s more to insight than what we’ve discussed. Turns out, this dichotomy between analytic problem-solving and insight problem solving doesn’t always hold up.
Sometimes insight can be reached via analytic thinking. Other times, you don’t need to have abandoned a problem to experience insight.6
Therefore, we need a novel way to look at insight that can account for these facts.
For that, I want you to think of problem-solving as going from point A (first encountering the problem) to point B (solving the problem).
Imagine that between points A and B, you have puzzle pieces scattered all around. Arranging these pieces in the right manner would be akin to solving the problem. You’ll have created a path from A to B.
If you encounter an easy problem, you’ve probably solved a similar problem in the past. You only need to arrange a few pieces in the right order to solve the problem. The pattern in which the pieces will fit together is easy to figure out.
This re-arranging of the pieces is analytic thinking.
Almost always, insight is experienced when you’re facing a complex problem. When the problem is complex, you’ll have to spend a long time re-arranging the pieces. You’ll have to take many trials. You’re playing with more pieces.
If you’re unable to solve the problem while you’re shuffling too many pieces, it leads to frustration. If you keep going and don’t abandon the problem, you might experience an insight. You finally found a pattern for the puzzle pieces that can lead you from A to B.
This feeling of having found a solution pattern to a complex problem produces insight, irrespective of whether you abandon the problem.

Think about how insight feels. It is pleasant, exciting, and brings relief. It is essentially a relief from overt or covert frustration. You’re relieved because you feel you’ve found a solution pattern for a complex problem- a needle in a haystack.
What happens when you abandon the problem?
As EII theory explains, it’s likely that you hand over sifting through the puzzle pieces to your unconscious mind in the process of implicitation. Just as you hand over cycling to your unconscious after you’ve done it for a while.
This is what’s likely to be responsible for that feeling of the problem lingering in the back of your mind.
While you’re engaged in other activities, the subconscious keeps re-arranging the puzzle pieces. It uses more pieces than you could’ve used consciously (activation of a wide range of concepts by the right hemisphere).
When your subconscious is done doing the re-arranging and believes it has reached a solution- a way to move from A to B- you get the “a-ha” moment. This solution pattern detection marks the end of a long period of frustration.
If you find that the solution pattern doesn’t actually solve the problem, you go back to re-arranging the puzzle pieces.
Re-structuring the approach, not the problem
Gestalt psychologists proposed that the incubation period helps the problem-solver to re-structure the problem i.e. see the problem itself differently.
In our puzzle pieces analogy, the pieces refer to elements of the problem, the problem itself, as well as the approach to solving the problem. So, when you’re re-arranging the puzzle pieces, you may do one or more of these things.
To highlight the difference between restructuring the problem itself and changing just the approach, I want to narrate an example from personal experience.
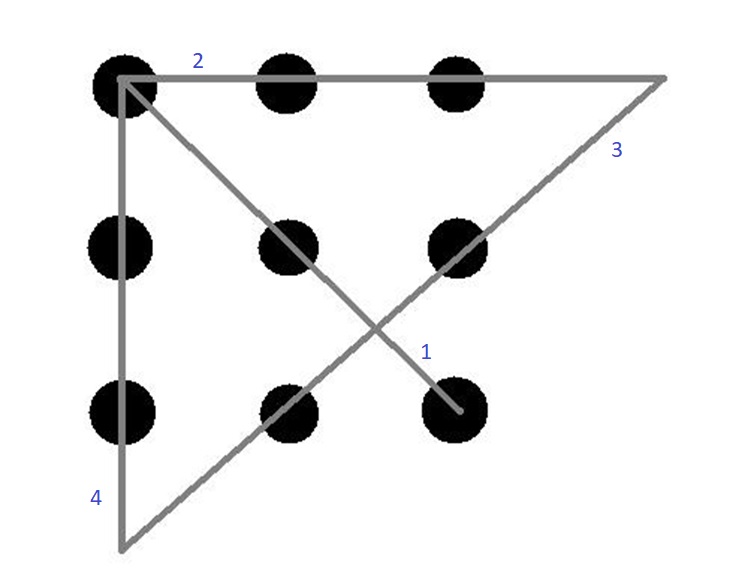
The 9-dot problem is a famous insight problem that requires you to think outside the box. When my father first showed this problem to me, I was clueless. I just couldn’t solve it. Then he finally showed me the solution, and I had an “a-ha” moment.

Since then, every time I’ve come across the problem, I’ve been able to solve it in just a few trials. The first time it took me many trials, and I failed.
Note that what I had learned from my “a-ha” moment was how to approach the problem differently. I didn’t re-structure the problem itself, only my approach to it. I didn’t memorize the solution. I just knew the right way to go about it.
When I knew the right way to approach it, I solved in a few trials every single time, despite not knowing what the solution looked like exactly.
This is true for so many complex problems in life. If some problem is taking you too many trials, perhaps you should reconsider how you’re approaching it before you start playing with other puzzle pieces.
References
- Ash, I. K., Jee, B. D., & Wiley, J. (2012). Investigating insight as sudden learning. The Journal of Problem Solving, 4(2).
- Wallas, G. (1926). The art of thought. J. Cape: London.
- Dodds, R. A., Smith, S. M., & Ward, T. B. (2002). The use of environmental clues during incubation. Creativity Research Journal, 14(3-4), 287-304.
- Hélie, S., & Sun, R. (2010). Incubation, insight, and creative problem solving: a unified theory and a connectionist model. Psychological review, 117(3), 994.
- Bowden, E. M., Jung-Beeman, M., Fleck, J., & Kounios, J. (2005). New approaches to demystifying insight. Trends in cognitive sciences, 9(7), 322-328.
- Weisberg, R. W. (2015). Toward an integrated theory of insight in problem solving. Thinking & Reasoning, 21(1), 5-39.
